Bagian 7 Pembangkitan Bilangan Acak

Simulasi atau pembangkitan bilangan adalah salah satu topik penting dalam statistika maupun bidang lain. Sangat sering kita ingin menerapkan prosedur statistika yang memerlukan pembangkitan atau pengambilan contoh angka acak.

7.1 Fungsi Peluang Suatu Sebaran

R dilengkapi dengan sekumpulan fungsi untuk membangkitkan bilangan acak yang memungkinkan kita untuk mensimulasikan sebaran peluang yang umum digunakan seperti Normal, Poisson, dan binomial dan lain-lain. Beberapa contoh fungsi untuk membangkitkan data yang berasal dari sebaran tertentu antara lain (Peng 2020):

rnorm: menghasilkan angka acak dengan rata-rata dan simpangan baku yang diberikan
dnorm: mengevaluasi kepekatan peluang normal (dengan rata-rata dan simpangan baku yang diberikan) pada suatu titik (atau vektor titik)
pnorm: mengevaluasi fungsi sebaran kumulatif untuk sebaran Normal
rpois: menghasilkan anka acak yang menyebar Poisson dengan tingkat tertentu

Dalam R, fungsi yang berhubungan dengan simulasi mengenai sebaran disusun dengan format <awalan><sebaran>. <awalan> berupa satu huruf sebagai berikut:

d untuk kepekatan peluang
r untuk membangkitkan peubah acak
p untuk sebaran kumulatif
q untuk fungsi quantile atau inverse

Sedangkan <sebaran> adalah nama sebaran (atau singkatannya) seperti norm, pois, unif dan lain lain. Selengkapnya di tabel berikut

Distribution	R name	Arguments
beta	`beta`	shape1, shape2, ncp
binomial	`binom`	size, prob
Chauchy	`cauchy`	location, scale
chi-squared	`chisq`	df, ncp
exponential	`exp`	rate
F	`f`	df1, df2, ncp
gamma	`gamma`	shape, scale
geometric	`geom`	prob
hypergeometric	`hyper`	m, n, k
log-normal	`lnorm`	meanlog, sdlog
uniform	`unif`	min, max
neg binomial	`nbinom`	size, prob
normal	`norm`	mean, sd
Poisson	`pois`	lambda
Student’s t	`t`	df, ncp

7.2 Teknik Pembangkitan Bilangan Acak

Teknik umum dalam pembangkitan bilangan acak antara lain 1. Inverse-transform method 2. Acceptance-rejection method 3. Direct Transformation

7.2.1 The Inverse Transform Method

Untuk membangkitkan contoh acak \(X\) dengan sebaran tertentu:

Tentukan fungsi sebaran kumulatif \(F(x)\) dari sebaran yang diinginkan
Hitung inverse dari \(F\) atau \(F^{-1}(x)\)
Bangkitkan contoh acak \(u_1, u_2, u_3, ..., u_n\) yang menyebar \(Seragam(0,1)\)
Hitung \(x_1 = F^{-1}(u_1)\), \(x_2 = F^{-1}(u_2)\), \(x_3 = F^{-1}(u_3)\), …, \(x_n = F^{-1}(u_n)\)

\(x_1, x_2, x_3\) merupakan contoh acak yang saling bebas dari peubah acak \(X\).

Contoh membangkitkan sebaran eksponensial.

Misal \(X \sim Eksponensial(\lambda)\)

Fungsi sebaran kumulatif

\[ F(X) = 1 - e^{-{\lambda}x}; \quad x \ge 0 \]

Fungsi inverse

\[ \begin{aligned} 1 - e^{-{\lambda}x} &= u \\ e^{-{\lambda}x} &= 1 - u \\ {-{\lambda}x} &= ln(1-u) \\ x &= -\frac{1}{\lambda}ln(1-u) \\ \end{aligned} \] Sehingga, \(F^{-1}(u) = -ln(1-u)/\lambda\)

Bangkitkan contoh acak \(Seragam(0,1)\)
Terapkan fungsi inverse untuk contoh acak yang telah dibangkitkan tersebut

7.2.1.1 Contoh 1

inv.exp <- function(u, lambda){
  -log(1-u)/lambda
}
  
rand.exp <- function(n = 1, lambda = 1){
  u <- runif(n)
  x <- inv.exp(u, lambda)
  return(x)
}

set.seed(123)
rand.exp(n = 10, lambda = 2)

##  [1] 0.16954209 0.77630468 0.26295011 1.07286505 1.41061464 0.02331342
##  [7] 0.37549990 1.11475582 0.40085086 0.30496835

set.seed(123)
X <- rand.exp(n = 1000, lambda = 2)

hist(X, freq=F, breaks =20, xlab='X', main='Contoh Acak Eksponensial')
curve(dexp(x, rate=2) , 0, 3, lwd=2, xlab = "", ylab = "", add = T)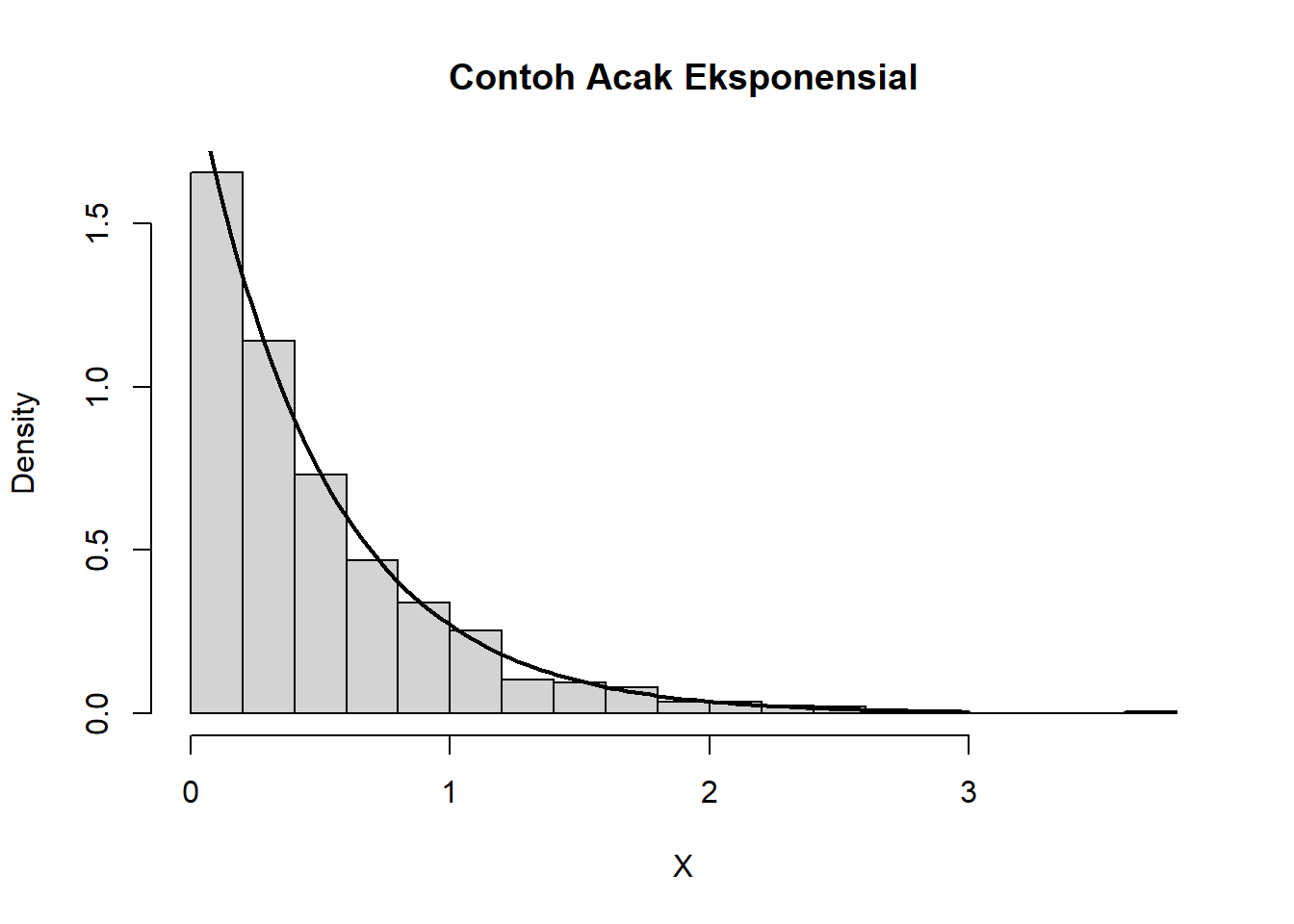

7.2.1.2 Contoh 2

Bangkitkan contoh acak dengan sebaran yang mempunyai fungsi kepekatan peluang

\[ f(x) = 3x^2, \quad 0 < x < 1 \]

Fungsi sebaran kumulatif

\[ F(x) = \int_0^x f_x(t)\,dt = x^3 \] Sehingga diperoleh fungsi inverse \(F^{-1}(u) = u^{1/3}\)

# http://www.di.fc.ul.pt/~jpn/r/ECS/index.html

inv.f <- function(u){
  u^(1/3)
}
  
inv.transform <- function(n = 1, inv.f){
  u <- runif(n)
  x <- inv.f(u)
  return(x)
}

set.seed(123)
X <- inv.transform(n = 10000, inv.f)

hist(X, freq=F, breaks =20, main="f(x)=" ~3*x^2~". Sample vs Density")
curve(3*x^2, 0, 1, lwd=2, xlab = "", ylab = "", add = T, col="red")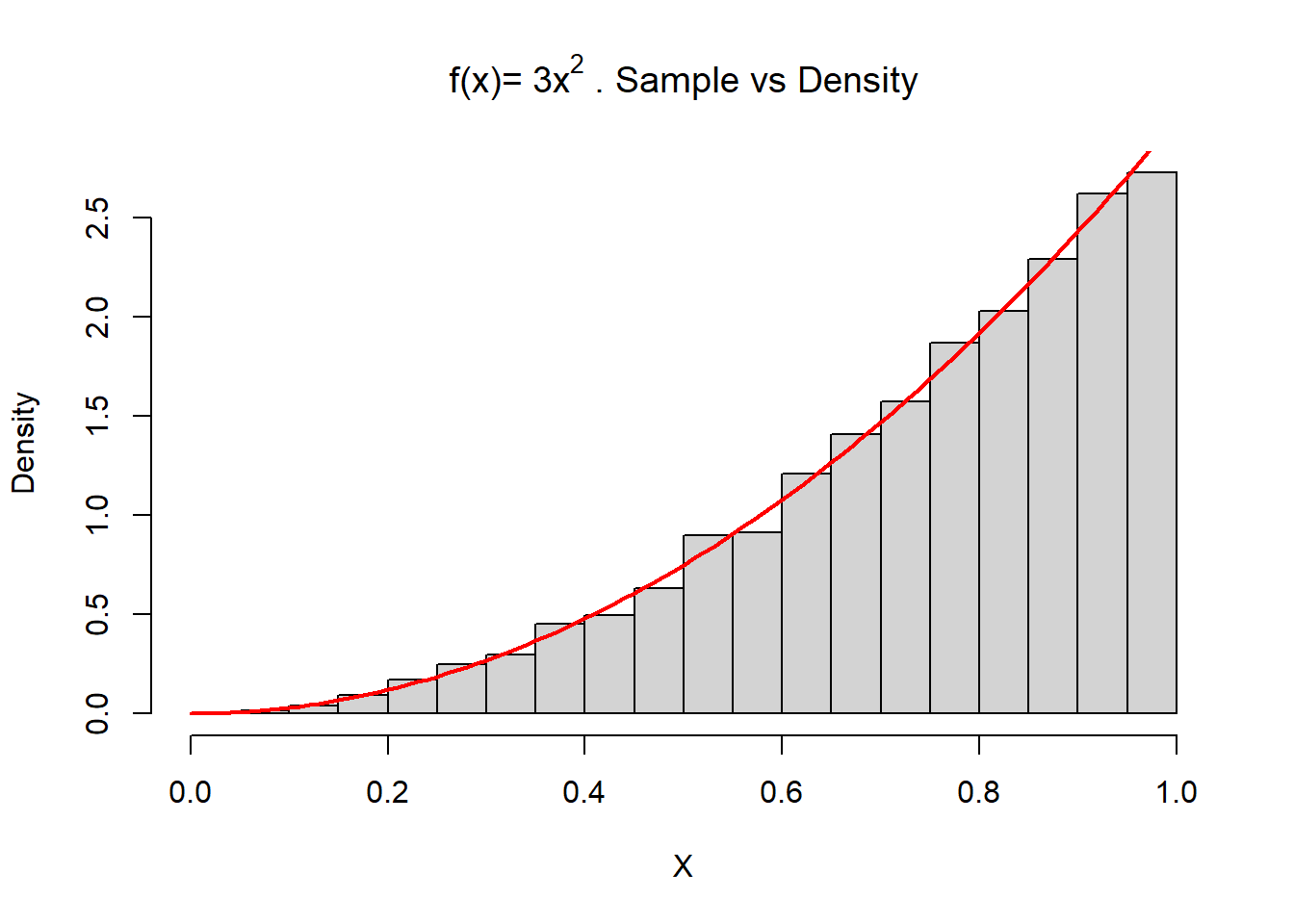

Referensi: (Bonakdarpour 2016) dan (Leonelli 2021)

7.2.2 Acceptance-Rejection Method

Algoritma untuk membangkitkan peubah acak \(X \sim f(x)\) di mana \(0 < x < x_1\) (dari responsi):

Bangkitkan \(x \sim U(x_0, x_1)\)
Tentukan \(c\) sehingga \(f(x) \le c\) untuk \(0 < x < x_1\)
Bangkitkan \(y_1 \sim U(0, c)\)
Tentukan \(y_2 = f(x)\)
Jika \(y_1 \le y_2\), terima \(x\)

7.2.2.1 Latihan 1 (Responsi)

Bangkitkan bilangan acak yang memiliki fkp \(f_Y(y) = 3y^2; \quad 0 < y < 1\) dengan menggunakan *acceptance-rejection method

ar <- function(n,x0,x1,f) {
  xx <- seq(x0,x1,length=10000)
  c <- max(f(xx))
  terima <- 0; iterasi <- 0
  hasil <- numeric(n)
  
while(terima<n) {
  x <- runif(1,x0,x1)
  y1<- runif(1,0,c)
  y2<- f(x)
  
if(y1<=y2) {
  terima <- terima+1
  hasil[terima]<-x }
  iterasi <- iterasi+1 }
  list(hasil=hasil,iterasi=iterasi)
}

set.seed(10)
f <- function(x) {3*x^2}
yyy <- ar(100,0,1,f)

par(mfrow=c(1,1))
hist(yyy$hasil,
main="f(x)="~3*x^2~" Sample vs Density", prob=T)
x <- seq(0, 1, 0.01)
lines(x, f(x), lwd=2, col="red")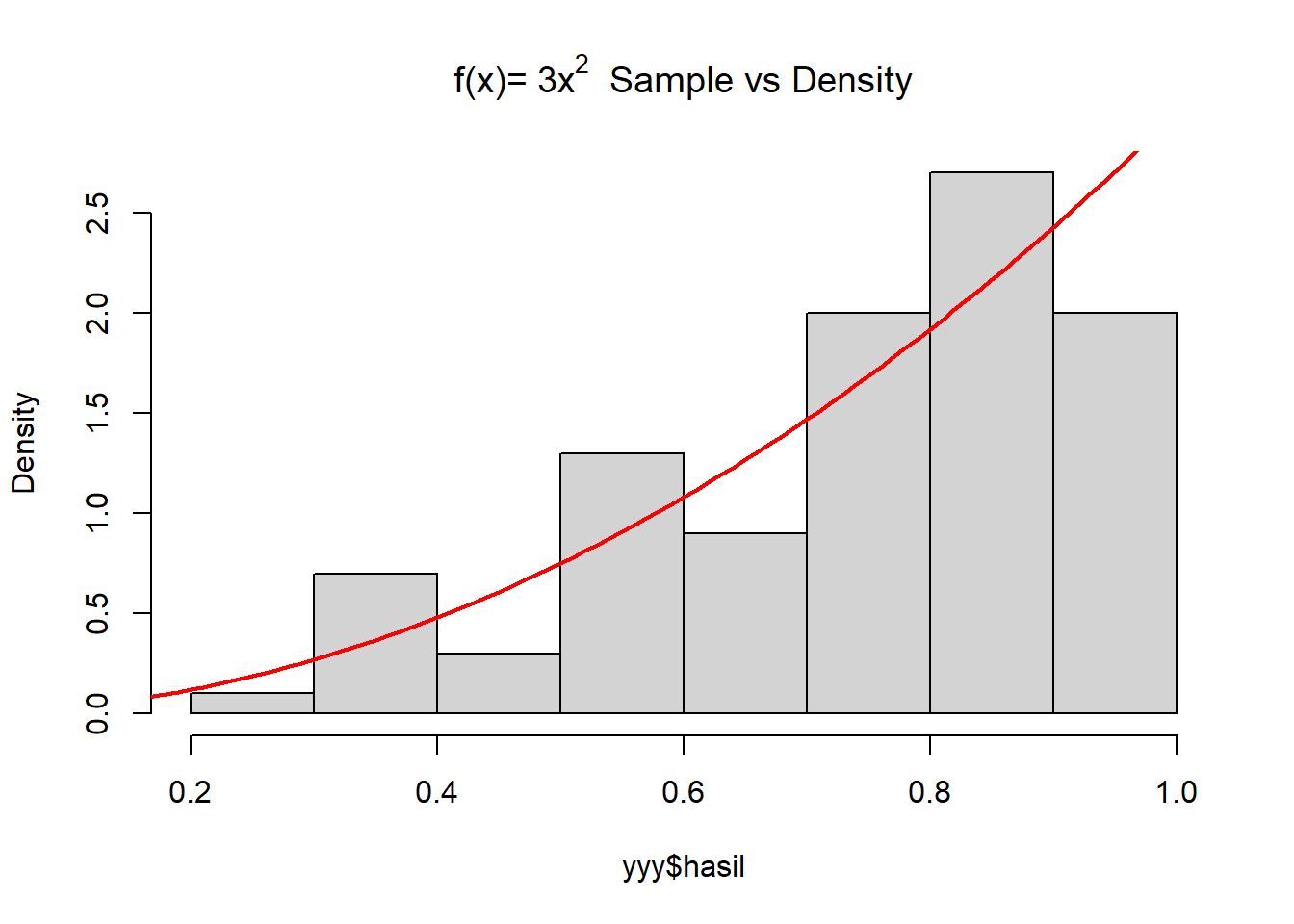

7.2.2.2 Contoh 2

Algoritma

Carilah peubah acak \(Y \sim g\) sehingga \(f(t)/g(t) \le c\) untuk semua \(t\) di mana \(f(t) > 0\)
Bangkitkan bilangan acak \(y\) dari sebaran dengan fungsi kepekatan/masa peluang \(g\)
Bangkitkan bilangan acak \(u\) dari sebaran \(Seragam(0,1)\)
Jika \(u < f(y)/(c.g(y))\), terima \(y\) sebagai bilangan acak, selainnya tolak \(y\) dan ulangi langkah 2-4

Bangkitkan peubah acak yang menyebar \(Beta(2,2)\)

# http://www.di.fc.ul.pt/~jpn/r/ECS/index.html

accept.reject <- function(f, c, g, rg, n) { 
  n.accepts     <- 0
  result.sample <- rep(NA, n)
  
  while (n.accepts < n) {
    y <- rg(1)               # step 1
    u <- runif(1,0,1)        # step 2
    if (u < f(y)/(c*g(y))) { # step 3 (accept)
      n.accepts <- n.accepts+1
      result.sample[n.accepts] = y
    }
  }
  
  result.sample
}

f  <- function(x) 6*x*(1-x)     # pdf of Beta(2,2), maximum density is 1.5
g  <- function(x) x/x           # g(x) = 1 but in vectorized version
rg <- function(n) runif(n,0,1)  # uniform, in this case
c  <- 2                         # c=2 since f(x) <= 2 g(x)

vals <- accept.reject(f, c, g, rg, 10000) 

hist(vals, breaks=30, freq=FALSE, main="Beta(2,2). Sample vs true Density")
xs <- seq(0, 1, len=100)
lines(xs, dbeta(xs,2,2), col="red", lwd=2)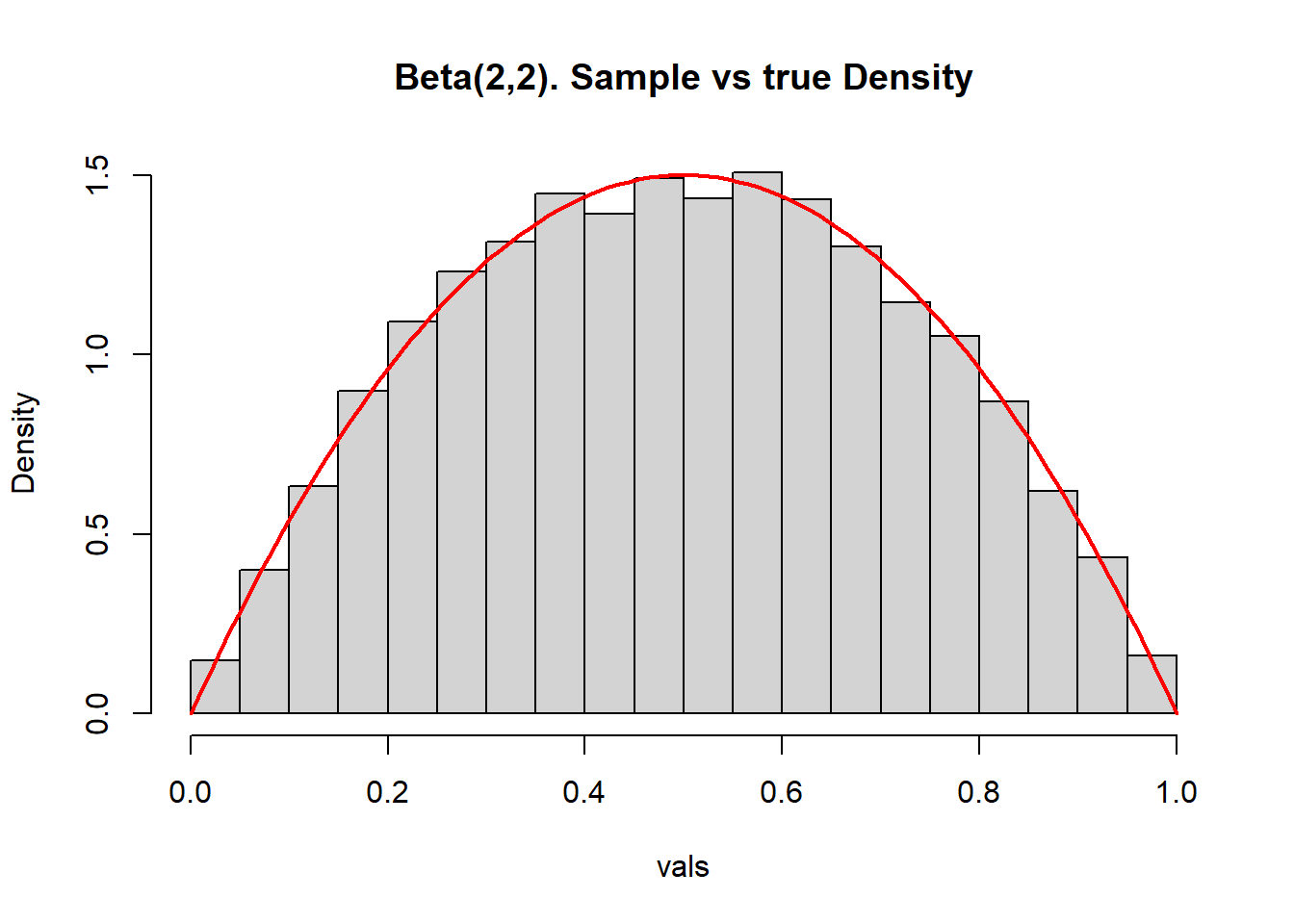

7.2.2.3 Contoh 3

Membuat sebaran “segitiga”

# triangle function
f  <- function(x){
  ifelse((0 < x) & (x < 1), x, 
         ifelse((1 <= x) & (x < 2), 2 - x, 0)) 
} 

g  <- function(x) x/x             # g(x) = 1 but in vectorized version
rg <- function(n) runif(n, 0, 2) # uniform, in this case. limit x from 0 to 2
c  <- 2                          # c=2 since f(x) <= 2 g(x)

vals <- accept.reject(f, c, g, rg, 10000) 

# Checking if it went well
hist(vals, breaks=30, freq=FALSE, main="Sample vs true Density")
xs <- seq(0, 2, len=100)
lines(xs, f(xs), col="red", lwd=2)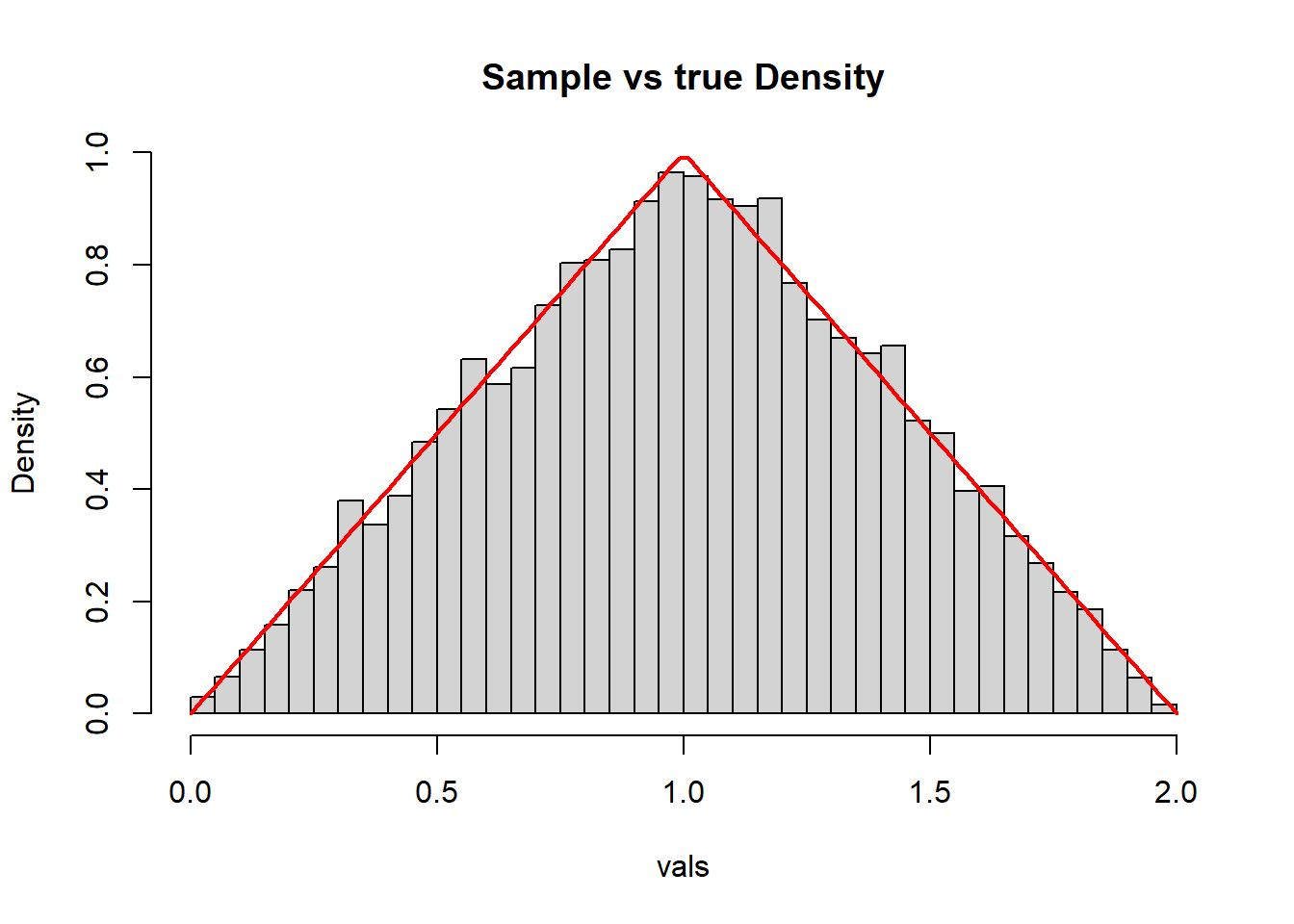

Dengan cara lain:

# https://users.phhp.ufl.edu/rlp176/Courses/PHC6089/R_notes/simulations.html

triangle.pdf = function(x){
  ifelse((0 < x) & (x < 1), x, 
         ifelse((1 <= x) & (x < 2), 2 - x, 0)) 
}

accept_reject = function(fx, n = 100) {
  #simulates a sample of size n from the pdf fx using the accept reject algorithm
  x = numeric(n)
  count = 0
  
  while(count < n) {
    temp <- runif(1, 0, 2)
    y <- runif(1, 0, 2)
    if (y < fx(temp)) {
      count = count + 1
      x[count] <- temp
    }
  }
  
  return(x)
}

data.sample = accept_reject(triangle.pdf, 10000)

hist(data.sample, breaks=30, freq=FALSE, main="Segitiga. Sample vs True Density")
xs = seq(-0.5, 2.5, by = 0.01)
lines(xs, triangle.pdf(xs), col="red", lwd=2)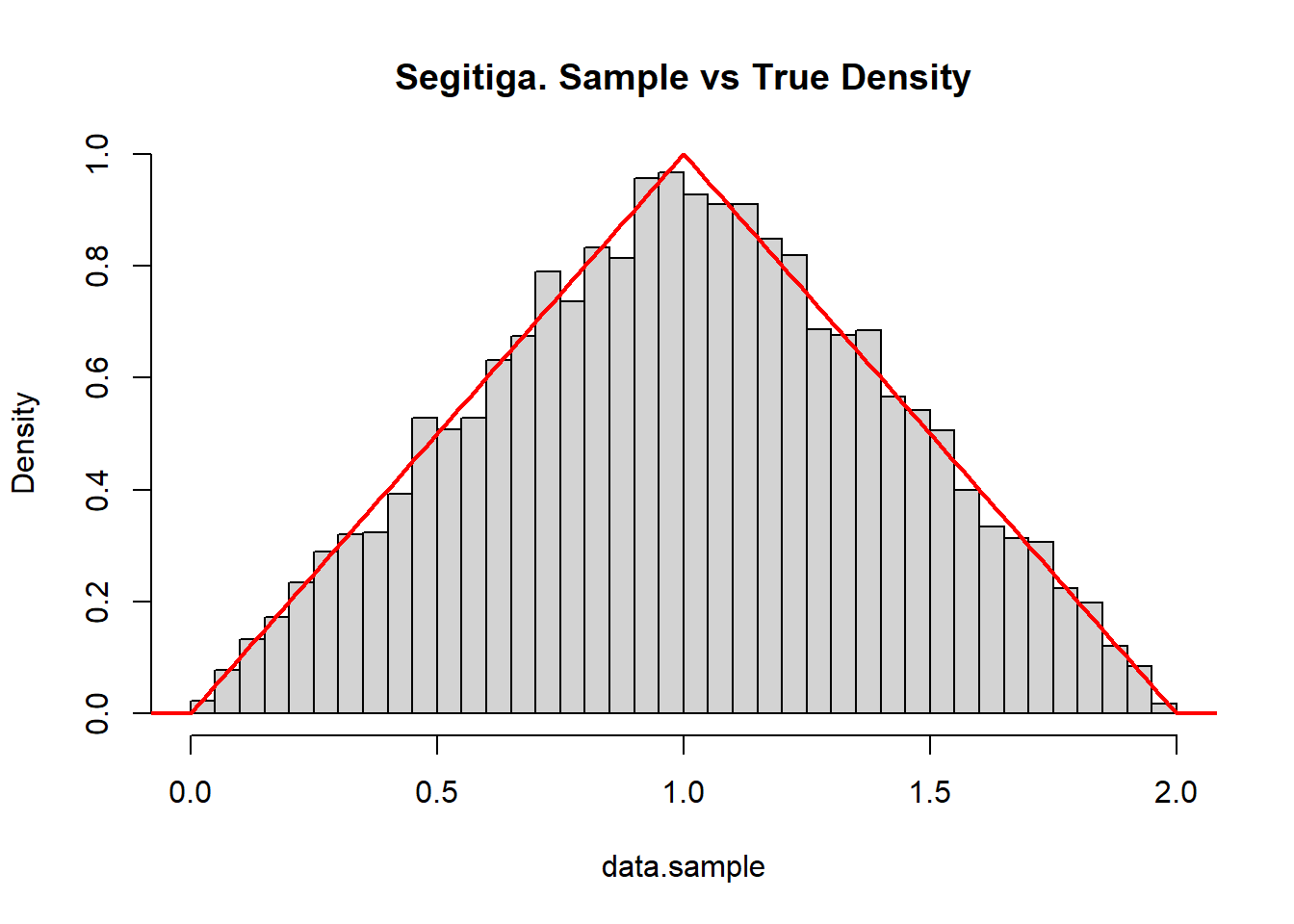

Referensi: (Neto 2014)

7.2.2.4 Contoh 4

Misalnya akan dibangkitkan bilangan acak dengan fungsi kepekatan peluang

\[ f(x) = \frac{3}{2}x^3 + \frac{11}{8}x^2 + \frac{1}{6}x + \frac{1}{12}; \quad 0 \le x \le 1 \]

f  <- function(x) (3/2)*(x^3)+(11/8)*(x^2)+(1/6)*(x)+(1/12) 
g  <- function(x) x/x             # g(x) = 1
rg <- function(n) runif(n, 0, 1)  # uniform, in this case
c  <- 4                           # 

vals <- accept.reject(f, c, g, rg, 10000) 

hist(vals, breaks=30, freq=FALSE, main="Beta(2,2). Sample vs true Density")
xs <- seq(0, 1, len=100)
lines(xs, f(xs), col="red", lwd=2)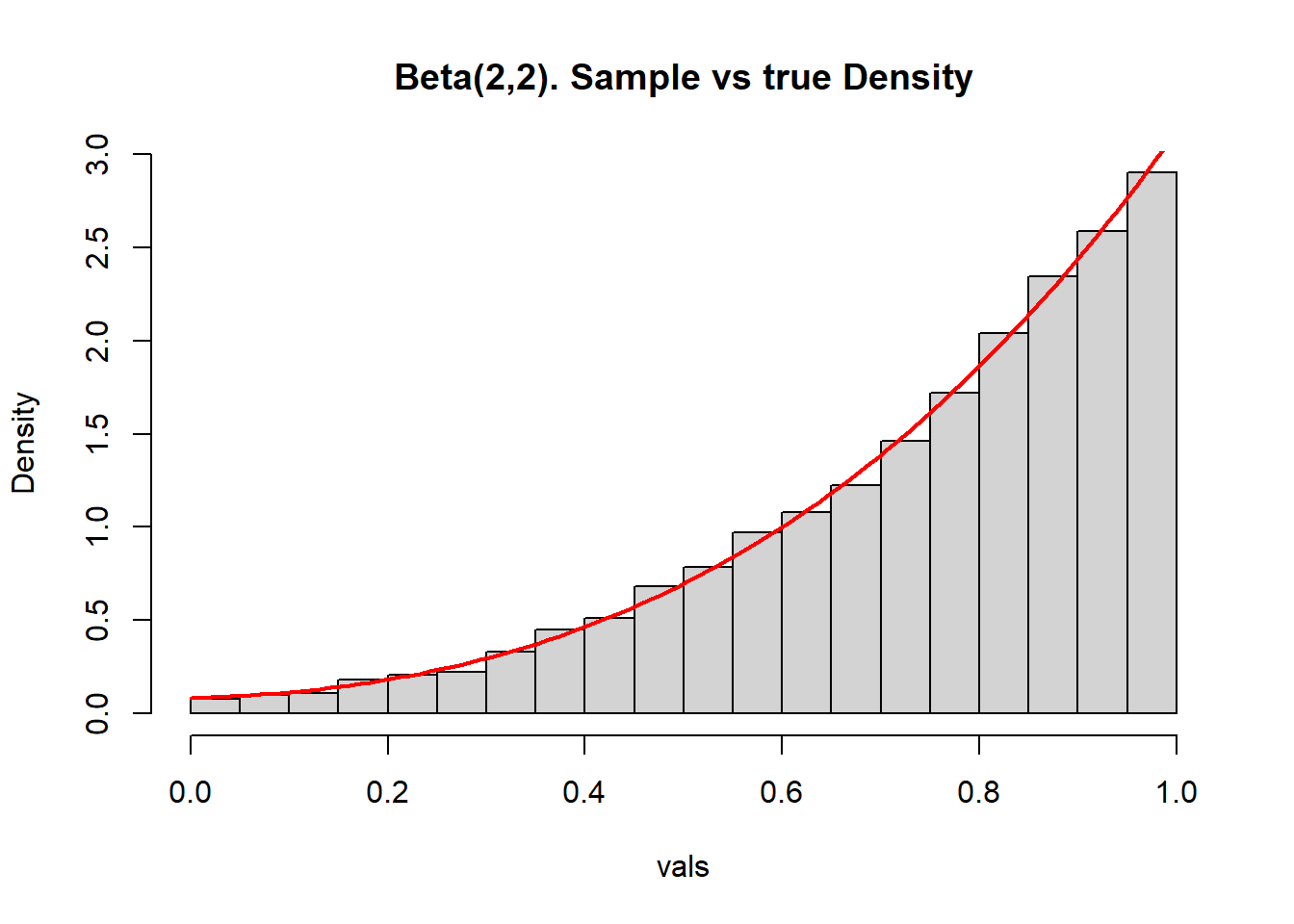

7.3 Membangkitkan Bilangan Acak untuk Regresi

7.3.0.1 Contoh 1

Bangkitkan bilangan acak untuk membangun persamaan regresi linier sederhana antara \(X\) terhadap \(Y\), dengan \(b_0 = 1, b_1 = 1\).

b0 <- 1
b1 <- 1

b0hat <- NULL
b1hat <- NULL

for (i in 1:100) {
  eps <- rnorm (10)
  X <- runif (10 ,5 ,10)
  Y <- b0 + b1*X + eps
  
  obj <- lm(Y~X)
  b0hat <- c(b0hat, obj$coefficients[1])
  b1hat <- c(b1hat, obj$coefficients[2])
}

hasil <- matrix (c(mean(b0hat), sd(b0hat), mean(b1hat) , sd(b1hat)), nrow =2, ncol =2)
rownames(hasil) <- c("mean","sd")
colnames(hasil) <- c("b0", "b1")
hasil

##            b0        b1
## mean 1.025390 0.9963052
## sd   1.712748 0.2302015

7.3.0.2 Contoh 2

Bangkitkan bilangan acak untuk membangun persamaan regresi linier berganda antara \(X_1\) dan \(X_2\) terhadap \(Y\), sehingga diperoleh \(b_0 = 10, b_1 = 2.3, b_2 = 0.7\).

set.seed(123)
X1 <- runif(25,10,25)
X2 <- runif(25,90,200)
Y <- 10 + 2.3*X1 + 0.7*X2 + rnorm(25,0,1)

model <- lm(Y~X1+X2)
summary(model)

## 
## Call:
## lm(formula = Y ~ X1 + X2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.64768 -0.51104 -0.05084  0.56224  2.28118 
## 
## Coefficients:
##             Estimate Std. Error t value             Pr(>|t|)    
## (Intercept) 8.819021   1.489143   5.922           0.00000584 ***
## X1          2.347724   0.045223  51.914 < 0.0000000000000002 ***
## X2          0.702732   0.006784 103.594 < 0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9363 on 22 degrees of freedom
## Multiple R-squared:  0.998,  Adjusted R-squared:  0.9978 
## F-statistic:  5509 on 2 and 22 DF,  p-value: < 0.00000000000000022

7.3.0.3 Contoh 3

Bangkitkan bilangan acak untuk membangun persamaan regresi linier berganda antara \(X_1\) dan \(X_2\) terhadap \(Y\), sehingga diperoleh \(b_0 = 1, b_1 = 1, b_2 = 1\).

library(MASS)

b0 <- 1
b1 <- 1
b2 <- 1

b0hat <- NULL
b1hat <- NULL
b2hat <- NULL

Sigma <- matrix(c(1 ,0.9 ,0.9 ,1),
                nrow =2 , ncol =2)
mu <- c(1 ,1)

for ( i in 1:100) {
  eps <- rnorm (10)
  X <- mvrnorm (10, mu, Sigma )
  Y <- b0 + b1*X [,1] * b2*X [,2] + eps
  
  obj <- lm( Y~X )

  b0hat <- c(b0hat, obj$coefficients[1])
  b1hat <- c(b1hat, obj$coefficients[2])
  b2hat <- c(b2hat, obj$coefficients[3])
}

hasil<- matrix(c(mean(b0hat), sd(b0hat), mean(b1hat), sd(b1hat), mean(b2hat), sd(b2hat)),
               nrow=2, ncol=3)
rownames(hasil) <- c("mean","sd")
colnames(hasil) <- c("b0", "b1", "b2")

hasil

##             b0        b1       b2
## mean 0.6721352 0.8529024 1.138359
## sd   1.2919187 1.5528197 1.597078

7.3.0.4 Contoh 4

Dari tugas kelompok

Bangkitkan peubah \(X_1\), \(X_2\), \(X_3\) sebanyak 1.000 amatan berdasarkan model regresi linear berganda berikut ini:

\[ Y = 10 + 3X_1 + 5X_2 + 7X_3 + \varepsilon \]

dengan mengasumsikan bahwa \(\varepsilon \sim N(\mu = 0, \sigma^2 = 30)\) dan antara peubah bebas terjadi multikolinearitas

Terdapat beberapa tahapan dalam melakukan pembangkitan data:

Mendefinisikan model regresi linier \(Y = 10 + 3X_1 + 5X_2 + 7X_3 + \varepsilon\)
Membuat matriks ragam peragam yang menunjukan korlasi antar peubah \(X\), di mana dalam simulasi ini nilai korelasi antar peubah adalah adalah 0.95 (korelasi tinggi sehingga terjadi multikolinearitas)
Membangkitkan data sisaan \(\varepsilon\) sebanyak 1.000 dengan mengasumsikan bahwa \(\varepsilon \sim N(\mu = 0, \sigma^2 = 30)\)
Menentukan nilai tengah peubah bebas sebesar 1
Membangkitkan peubah \(X\) dan menghitung peubah \(y\)

# membuat fungsi untuk membangkitkan bilangan acak multivariate normal
# dengan korelasi tertentu
rmvn.eigen <- function(n, mu, Sigma) {
  d <- length(mu)
  ev <- eigen(Sigma, symmetric = TRUE)
  lambda <- ev$values
  V <- ev$vectors
  R <- V %*% diag(sqrt(lambda)) %*% t(V)
  Z <- matrix(rnorm(n*d), nrow = n, ncol = d)
  x <- Z %*% R + matrix(mu,n,d, byrow = T)
  
  return(x)
}

# jumlah pengamatan
n <- 1000
# rataan peubah penjelas
mu <- c(0,0,0)
# matriks ragam-peragam
Sigma <- matrix(c(1,    0.95, 0.95,
                  0.95, 1   , 0.95,
                  0.95, 0.95, 1  ), nrow = 3, ncol = 3)

# membangkitkan bilangan (X dan sisaan)
set.seed(5555)
x <- rmvn.eigen(n, mu, Sigma)
eps <- rnorm(n,0,sqrt(30))
colnames(x) <- paste0("X", seq(length(mu)))

# menentukan beta, dan membangkitkan Y
beta <- c(b0 = 10, b1 = 3, b2 = 5, b3 = 7)
y <- round(beta[1] + (x %*% beta[-1]) + eps, 4)

Periksa hasil

# matriks korelasi
cor(x)

##           X1        X2        X3
## X1 1.0000000 0.9519284 0.9474503
## X2 0.9519284 1.0000000 0.9487071
## X3 0.9474503 0.9487071 1.0000000

dataRegresi <- data.frame(y, x) 
# analisis regresi
reg <- lm(y ~., data = dataRegresi)
reg

## 
## Call:
## lm(formula = y ~ ., data = dataRegresi)
## 
## Coefficients:
## (Intercept)           X1           X2           X3  
##      10.353        2.826        4.412        7.831